
✔ 분류란?
학습 데이터로 주어진 데이터의 피처와 레이블값(결정 값, 클래스 값)을 머신러닝 알고리즘으로 학습해 모델을 생성하고 이렇게 생성된 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측하는 것이다.
분류를 구현하는 알고리즘
- 나이브 베이즈
- 로지스틸 회귀
- 결정 트리
- 서포트 벡터 머신
- 최소 근접 알고리즘
- 신경망
- 앙상블
이 중, 이미지, 영상, 음성, NLP 영역에서 신경망에 기반한 딥러닝이 머신러닝계를 선도하고 있지만,
이를 제외한 정형 데이터의 예측 분석 영역에서는 👉 앙상블이 매우 높은 예측 성능으로 인해 많은 분석가와 데이터 과학자들에게 애용되고 있다.
✔ 앙상블이란?
- 서로 다른/또는 같은 알고리즘을 단순 결합한 형태도 있음 (대부분 동일한 알고리즘을 결합)
- 일반적으로 배깅과 부스팅 방식으로 나뉨
- 앙상블은 여러 개의 약한 학습기(예측 성능이 상대적으로 떨어지는 학습 알고리즘)를 결합해 확률적 보완과 오류가 발생한 부분에 대한 가중치를 계속 업데이트하며 예측성능을 향상함
결정 트리

- ML 알고리즘 중 직관적으로 이해하기 쉬운 알고리즘
- 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만듦
- 사이킷런 알고리즘 : DecisionTreeClassifier & DecisionTreeRegressor (여기서는 분류만 확인)
- 구조
- 규칙 노드 : 규칙 조건 (이미지에서 Decision Node)
- 리프 노드 : 결정된 클래스 값
- 서브 트리 : 새로운 규칙 조건마다 생성되는 트리형 구조
- 중요한 지표 : 균일도
- 균일도는 데이터를 구분하는데 필요한 정보의 양에 영향을 미침
- 결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 만듦
- 정보의 균일도를 측정하는 대표적인 방법 : 엔트로피를 이용한 정보 이득 & 지니 계수
- DecisionTreeClassifier는 기본적으로 지니계수를 이용해 데이터 세트를 분할
- 데이터가 모두 특정 분류에 속하게 되면 분할을 멈추고 분류를 결정
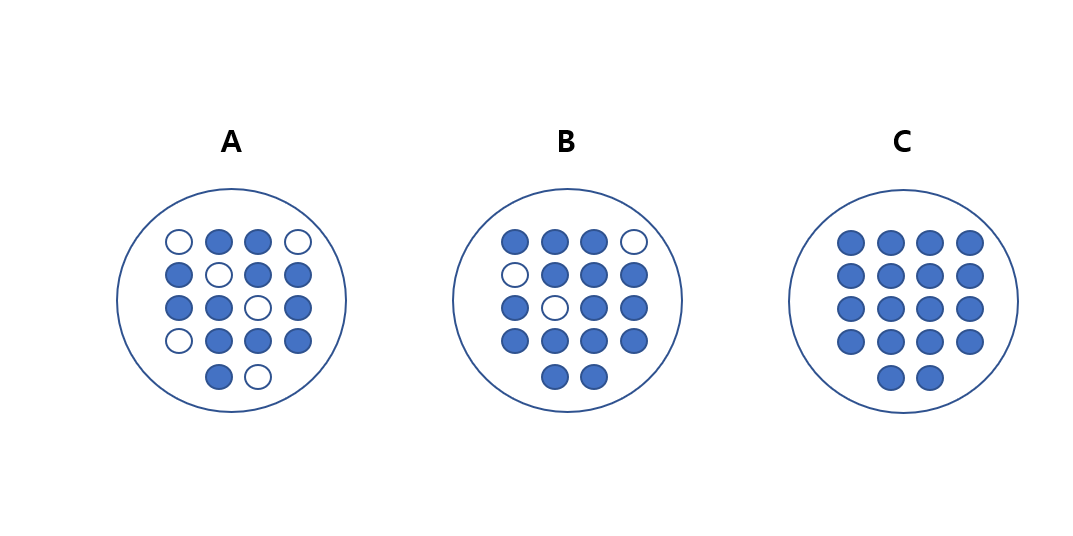
# 지니 계수와 엔트로피
▶ 정보 이득 = 1 - 엔트로피 (데이터 집합의 혼잡도)
▶ 지니 계수 : 0이 가장 평등하고 1로 갈수록 불평등 >> 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석
결정 트리 모델의 특징
- 정보의 '균일도'라는 룰을 기반으로 하여, 알고리즘이 쉽고 직관적
- 정보의 균일도만 신경 쓰면 되므로, 각 피처의 스케일링과 정규화 같은 전처리 작업이 필요하지 않음
- 하지만, 과적합으로 정확도가 떨어질 수 있음
- 트리의 크기를 사전에 제한하는 것이 오히려 성능 튜닝에 더 도움이 됨
사이킷런의 결정 트리 알고리즘과 하이퍼 파라미터
- 사이킷런의 결정 트리 구현은 CART(Classification And Regression Trees) 알고리즘 기반으로, 분류와 회귀에서 모두 사용됨
- 본 포스팅에서는 분류를 위한 DecisionTreeClassifier 클래스만 다룸(회귀에서도 동일한 파라미터를 사용함)
- 파라미터 옵션을 지정하지 않으면 과적합 위험이 매우 크므로, 반드시 제어가 필요하다
| 파라미터 명 | 설명 |
| min_samples_split | - 노드를 분할하기 위한 최소한의 샘플 데이터 수 ➡ 과적합 제어용 - 디폴트 : 2 - 작게 설정할수록 과적합 가능성 증가 |
| min_samples_leaf | - 분할이 될 경우 왼쪽과 오른쪽 브랜치 노드에서 가져야 할 최소한의 샘플 데이터 수 ➡ 과적합 제어용 - 큰 값으로 설정할 수록 과적합 가능성 감소 - 단, 비대칭적 데이터의 경우 작게 설정 필요 |
| max_features | - 최적 분할을 위해 고려할 최대 피처 수 - 디폴트 : None(모든 피처를 고려함) - int(정수형)로 개수 지정 - float 형으로 대상 피처의 퍼센트를 지정 - sqrt : 전체 피처 개수의 제곱근 - auto : sqrt 와 동일 - log : log2(전체 피처 개수) |
| max_depth | - 트리의 최대 깊이 지정 - 디폴트 : None(완벽하게 클래스 결정할 때까지 깊이 계속 키움) - 디폴트로 두면 과적합 위험이 있으니, 적절한 값으로 제어 필요 |
| max_leaf_nodes | - 말단 노드의 최대 개수 |
[ 예제 ] iris 데이터로 결정 트리 수행 & 중요한 피처 확인
- 결정 트리는 균일도에 기반해 어떠한 속성을 규칙 조건으로 선택하느냐가 중요한 요건이다. 중요한 몇 개의 피처가 명확한 규칙 트리를 만드는 데 크게 기여하며, 모델을 좀 더 간결하고 이상치에 가한 모델을 만들 수 있기 때문이다.
- feature_importances_ 속성으로 결정트리에서 더 중요한 피처를 확인할 수 있다.
- ndarray 형태로 값을 반환하며, 피처 순서대로 값이 할당됨
- 일반적으로 값이 높을수록 해당 피처의 중요도가 높다는 뜻
- 시각화를 통해 중요도 차이를 확인 >> petal length 중요도가 가장 큼
import seaborn as sns
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# DecisionTree Classifier 생성
dt_clf = DecisionTreeClassifier(criterion = 'entropy', random_state=156)
# 붓꽃 데이터를 로딩하고, 학습과 테스트 데이터 셋으로 분리
iris_data = load_iris()
X_train , X_test , y_train , y_test = train_test_split(iris_data.data, iris_data.target,
test_size=0.2, random_state=11)
# DecisionTreeClassifer 학습.
dt_clf.fit(X_train , y_train)
# feature_importance_ 추출
print("Feature importance:\n{0}" .format(np.round(dt_clf.feature_importances_, 3)))
# feature 별 importance 매핑
for name, value in zip(iris_data.feature_names, dt_clf.feature_importances_):
print(name, value)
sns.barplot(x = dt_clf.feature_importances_, y = iris_data.feature_names)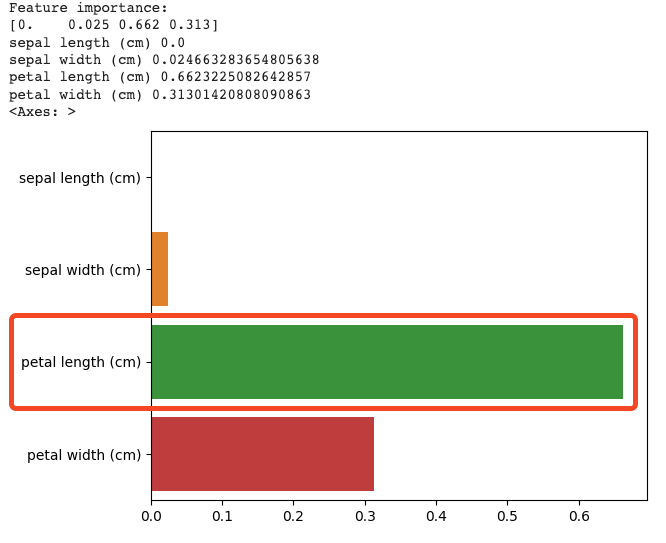
728x90
'Machine Learning > scikit-learn' 카테고리의 다른 글
| [앙상블] 앙상블의 개념과 보팅(하드보팅 vs. 소프트 보팅) (0) | 2023.08.22 |
|---|---|
| 결정 트리 실습 - 사용자 행동 인식 데이터 분류 예제 (0) | 2023.08.21 |
| [이진 분류_성능 평가 지표] 정밀도 / 재현율 (0) | 2023.08.20 |
| [분류_성능 평가 지표] 정확도와 오차 행렬(이진 분류) (0) | 2023.08.18 |
| [GridSearchCV] 교차 검증 & 하이퍼 파라미터 튜닝을 한 번에 (0) | 2023.08.17 |



